Discover the Significance of Matching the Sensor Size and Pixel Size to a Lens's MTF
In this article, we will explore lenses' MTF curves at various spatial frequencies and determine the lens that best aligns with the sensor size and pixel size of your camera.
This article, Understanding the use of MTF in evaluating lens quality, offers valuable introductory knowledge about MTF graphs that you may find helpful before continuing
Matching the Sensor Size to the MTF
Choosing a lens with the appropriate coverage for your camera's sensor ensures that the image quality is maintained across the entire frame. This means that the selected lens must produce an image circle that is of sufficient size to cover the camera's sensor.
Case Study
Let's take a deeper look at selecting a suitable lens while considering the image circle.
Given two lenses: Lens Pyrite 4.0/45 and Lens Pyrite 4.5/90, we will select the most suitable lens for a camera with a sensor size of 42mm. And for a simple comparison, let's assume that the aperture of the lens is fixed at f/5.6.
Comparing the camera's sensor size of 42 mm with the lenses' image circles, we notice that:
Lens PYRITE 4.0/45 has an image circle of 43.2 mm, allowing the full image circle area to be used
Lens PYRITE 4.5/90 has an image circle of 90 mm, meaning only half of the image circle will be used. Therefore areas shown in black are not in use, and only the remaining MTF values are applied.
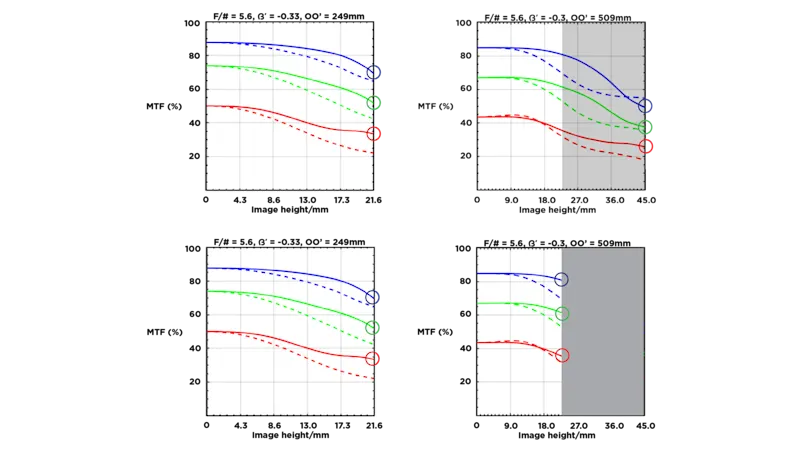
Results of the lens comparison
As shown in the above illustration: without considering the image circle, the MTF graphs of both Lens PYRITE 4.0/45 and Lens PYRITE 4.5/90 show similar performance.
However, when the image circle is considered, the MTF values for a camera with a sensor size of 42mm are more uniform across the Lens PYRITE 4.5/90, rather the Lens PYRITE 4.0/45, therefore making the Lens PYRITE 4.5/90 the better lens in this case.
Relationship between a Lens's image circle and its resolution
In this section, we will explore how differences in image quality occur and investigate the relationship between the lens's image circle and its resolution.
The two photos below were taken of the same scene using different lenses, both with a 50mm focal length and using the same f-number. Both lenses have the same image circle, which is a good match for the camera's sensor size.
However, there is a noticeable difference in image quality between the two photos. Let's find out what causes this difference.
To understand the relationship between a lens's resolution and the resulting image quality, consider the following three simulated images of a teddy bear. These images were captured using the same camera sensor size (using lenses with matching image circles), but with different lens resolutions. While the sensor size remains the same, as the resolution increases, the pixel size becomes smaller. This difference in pixel size can affect the overall image quality and the achievable level of detail.
You can see that when the camera sensor has lower resolution (meaning larger sensor pixels) there is not a significant difference in the images produced by the two lenses. However, as the pixel size decreases, differences in the resulting image quality become more noticeable. Ultimately, the final image quality of the two lenses is affected as the pixel size decreases, displaying the difference in their performance characteristics.
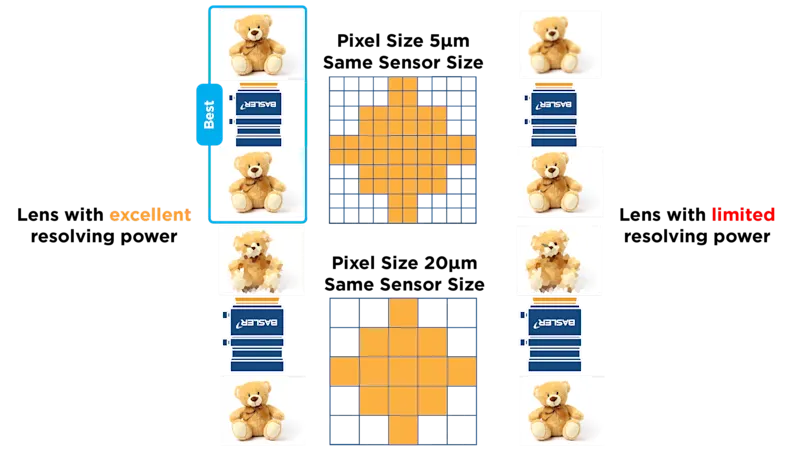
About Airy Disks - Why does pixel size affect the image quality?
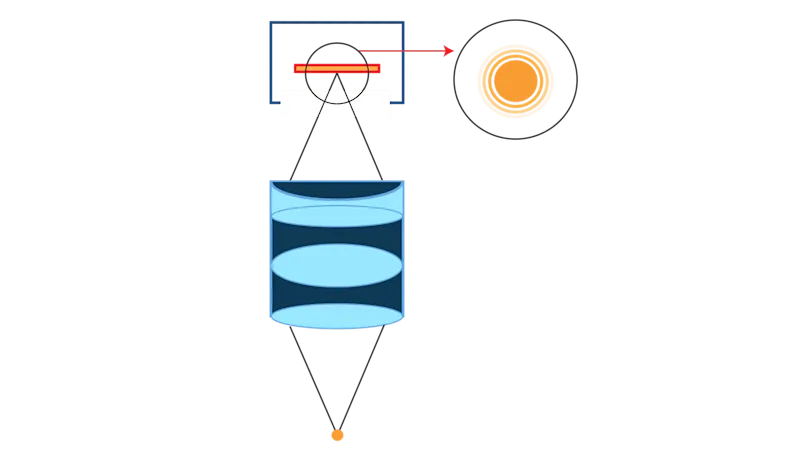
When your subject includes a point source, it passes through the lens and forms an Airy disk on the sensor as opposed to a focused point. This Airy disk appears as a series of concentric circles. If the size of the first circle of the Airy disk is smaller than the sensor's pixel size, it will be represented by a single pixel.
Consequently, when comparing two lenses with different performance characteristics, each lens will create a different sized Airy disk on the sensor.
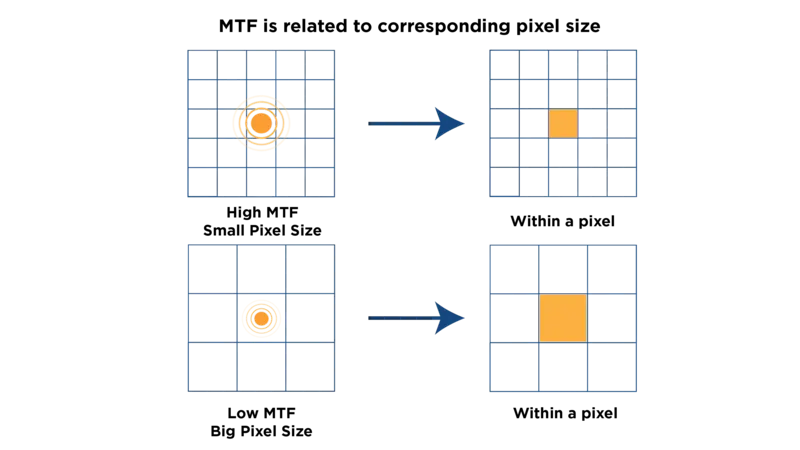
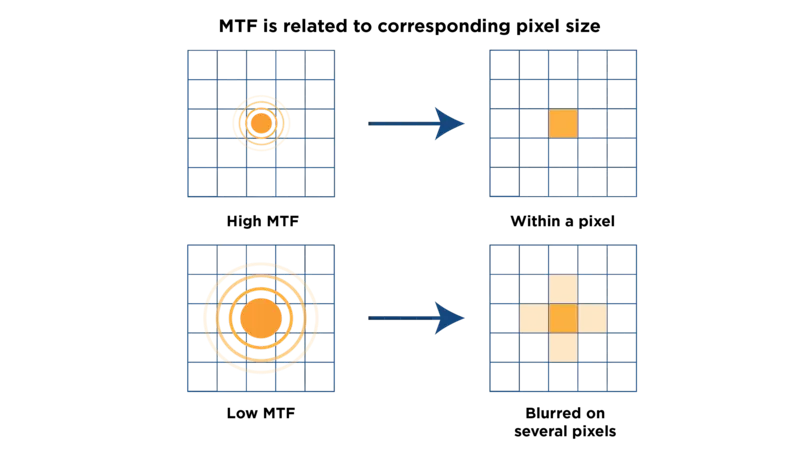
There will not be a noticeable difference in the resulting image quality if sensor's pixels are larger than both of these Airy disk sizes.
This is why lower-resolution cameras with larger sensor pixels, such as those found in older cameras, do not demonstrate a significant difference in image quality between a high-resolution lens and a low-resolution lens. However, as camera resolution increases, and the sensor pixel size becomes smaller than one of the Airy disks' sizes, the lens with the larger Airy disk will produce an image blur in the final image.
Matching Pixel Size to MTF
Matching a camera sensor's pixel size to the modulation transfer function (MTF) of a lens is an important consideration in digital imaging. The goal is to optimize the system's performance by ensuring that the lens and sensor work well together to capture the maximum amount of detail. For the best system performance, it is very important that both the lens and the camera have similar resolution.
Let's use MTF to calculate the appropriate pixel size:
MTF = (lp/mm) = 1000/(2×pixel size (µm)) or Pixel size (µm) = 1000/(2×(lp/mm))
If the MTF is 50 lp/mm @ 30% contrast, this means there are 50 line pairs in 1 mm;
Pixel size (µm) = 1000/(2×(50) )=10 µm
If the MTF is 100 lp/mm @ 30% contrast, this means there are 100 line pairs in 1 mm;
Pixel size (µm) = 1000/(2×(100) )=5 µm
If a lens has a MTF performance of 50 lp/mm, it can be matched to a 10 µm pixel size. Meanwhile, if a lens has a MTF performance of 100 lp/mm, it is suitable for a camera with 5 µm pixel size.
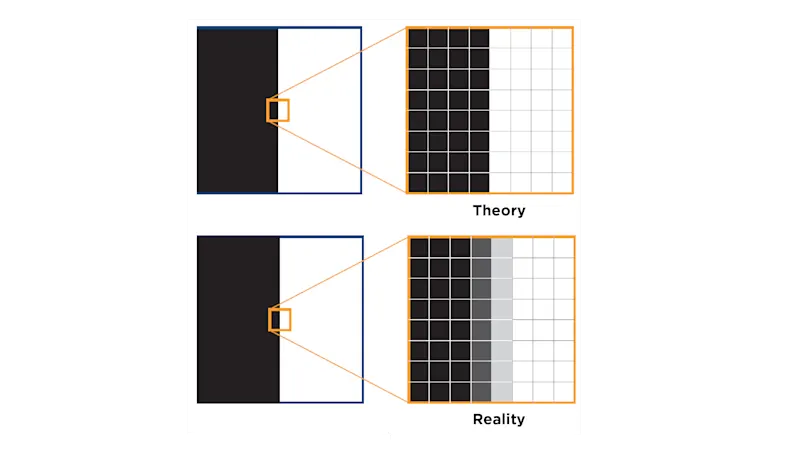
An ideal resolution means that the boundaries between black and white lines are perfectly sharp. Of course, theory always differs from reality, and so in reality these boundaries blur into gray tones ranging from white to black. The lower the lens resolution, the less sharp the transition. And the less sharp the transition, the lower the "contrast".
When looking at resolution, whether it's measured in megapixels, line pairs per millimeter, or meters, it's important to consider contrast as well. Manufacturers typically specify a contrast of 30%, which is a good balance for image sharpness. This means that a 30% contrast MTF (Modulation Transfer Function) value is considered a good standard for assessing sharpness.
Practical MTF (lp/mm) = 1/(2 x pixel size x 0.7)
Case Study:
Let's take a deeper look by evaluating the suitability of a lens for a camera with a given pixel size.
Given a camera with a pixel size of 7µm, how well will a Lens Pyrite 4.5/90 match the camera?
If the MTF is 40 lp/mm @ 68% contrast, this means there are 40 line pairs in 1 mm;
Pixel size (μm) = 1000/ 2 x 40 x 0.7 = 8.75 μm
If the MTF is 80 lp/mm @ 44% contrast, this means there are 80 line pairs in 1mm;
Pixel size (μm) = 1000 / 2 x 80 x 0.7 = 4.375 μm
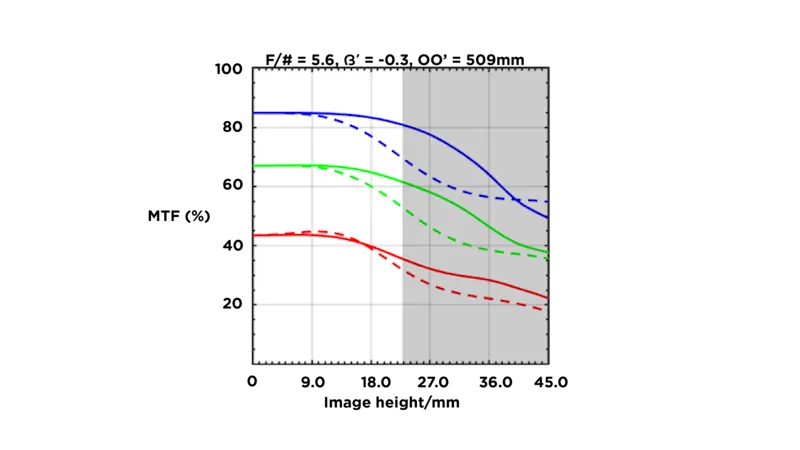
Based on this evaluation with the MTF curve, if the application required 40 lp/mm with 60% contrast, then the Lens Pyrite 4.5/90 will meet the requirement.
However, if the application required 80 lp/mm with more than 50% contrast, the Lens Pyrite 4.5/90 would not be suitable. This lens choice would affect the overall image quality by capturing a lower level of detail.
Conclusion
Understanding the Modulation Transfer Function (MTF) characteristics of a lens along with the camera's sensor size and pixel properties is crucial for achieving optimal image quality. Matching a lens's MTF curves to the sensor size and pixel size of the camera helps ensure compatibility and maximize image sharpness.
When selecting a lens, consider its image circle coverage to ensure that the entire sensor area is utilized to provide consistent image quality across the frame. A lens that produces an image circle covering the entire camera sensor is ideal.
When comparing lenses based on MTF graphs alone, recall that the lenses may seem similar in performance, but it is important to select the one with the image circle that best matches the sensor size of the camera. It will typically provide better image quality.
The relationship between lens resolution and image circle affects image quality. As pixel size decreases, differences in lens resolution become more noticeable. This impacts the level of detail captured in the final image.
Matching sensor pixel size to lens MTF is important for optimizing system performance. Calculate the appropriate pixel size based on the lens's MTF performance to ensure the best image quality.
In conclusion, understanding the relationship between a lens's MTF and a camera's sensor size and pixel properties is essential for selecting the right lens for your camera system— and achieving the best possible image quality.
Our lenses & matching accessories
Take advantage of our broad portfolio and choose the right product for your vision system. Ourlens selector helps you to easily choose the right lens for your overall system.
