顕微鏡システムの分解能を制限する4つの要因
回折限界、レイリー基準、光学収差、ナイキストの定理
高精細顕微鏡システムを開発するには、理論的・実践的観点から光学上の制約を正しく理解する必要があります。以下では、ビジョンエンジニアを対象に、顕微鏡システムの分解能を制限する4つの要因について詳しく解説します。

1. 顕微鏡システムの分解能
顕微鏡システムの分解能は、対象物をどこまで細かく識別できるかを示す指標です。カメラの画素数がどれほど高くても、分解能が低ければ、光学的な結像限界によって微細な構造物を可視化できません。そのため、半導体検査など高精度な撮像が求められる用途では、分解能が非常に重要になります。
顕微鏡システムの分解能を制限する要因には、回折限界、レイリー基準、光学収差、ナイキストの定理の4つがあり、それぞれが画質と深く関わっています。
2. 回折限界:物理的な絶対限界

アッベの回折限界
1873年にエルンスト・アッベによって提唱された回折限界は、光の波長に起因する分解能の物理的な絶対限界を示したもので、d=λ÷(2×NA)の計算式で表されます。
d:分解可能図形寸法(分解能)
λ:光の波長
この計算式からわかる通り、分解能を向上させるには、より短い波長の光とより高い 開口数(NA) が必要です。そのうち、開口数は、媒質の屈折率と集光角度によって決まります。
例えば、500nmの波長の光と開口数1.4の油浸対物レンズを使用する場合、顕微鏡システムの理論上の分解能(横方向分解能)は179nmになります。しかし、複数波長の光の混在やレンズ設計の違いなどを考慮すると、実際の分解能は200nmまで低下します。
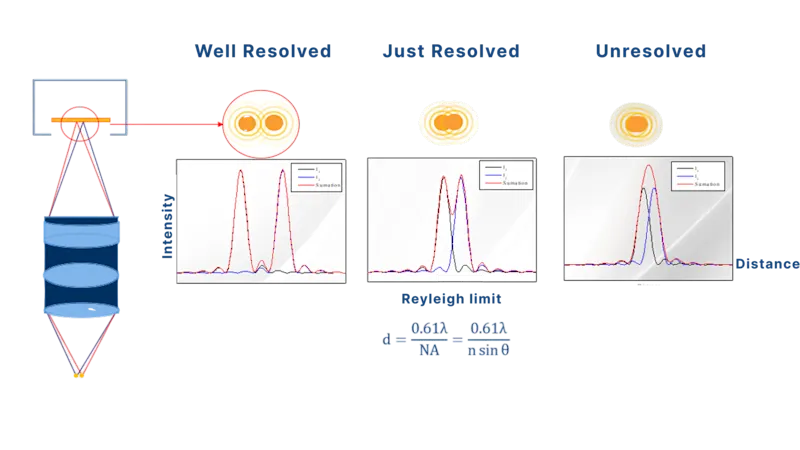
レイリー基準
アッベの回析限界が理論上の分解能を示しているのに対し、2つの輝点を識別できる最小距離を示しているのがレイリー基準です。レイリー基準では、エアリーディスクの中心部(最輝部)と一番内側の暗環(暗い同心円環)が重なっていれば、2つの輝点は分離状態にあると定義しており、d=0.61λ÷NAの計算式で表されます。
低コヒーレント光または非コヒーレント光を使用し、周囲と異なる物体を可視化する場合(粒子の検出、汚染物質の分析など)は、レイリー基準が特に有用です。また、多くの産業用レンズの製品仕様書には、「レイリー分解能:0.85µm(550nm時)」といった記載があるため、これらの数値から必要なコントラストを把握したうえで、検査の自動化・精度向上に役立てるとよいでしょう。
理論上の分解能を示しているアッベの回折限界と、2つの輝点を識別できる最小距離を示しているレイリー基準は、互いに補完関係にあります。光の波長、対物レンズの開口数などのシステム要件を決定する時はアッベの回折限界、撮影に必要なコントラストが知りたい時や、物体が分離しているかどうかを確認する時はレイリー基準を参考にするとよいでしょう。両方の考え方を取り入れれば、顕微鏡システムの分解能と画質のバランスを最適化することができます。
3. 光学収差:不可避の物理現象
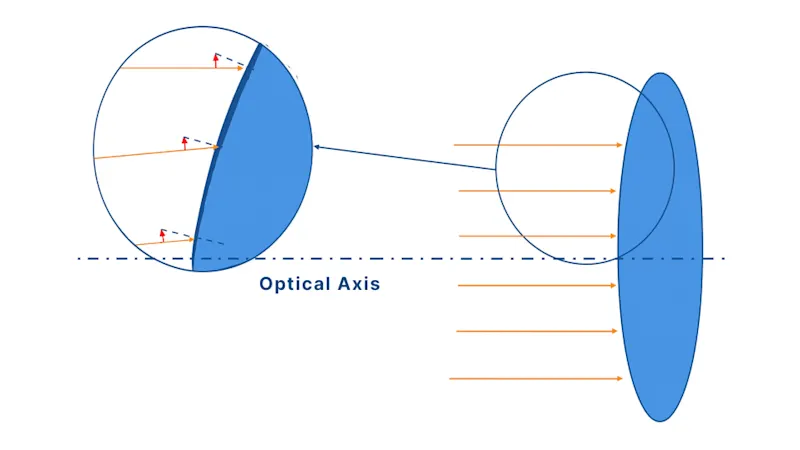
アッベの回折限界とレイリー基準を考慮して顕微鏡システムを設計したとしても、実際の撮影において、光学収差を完全に排除することはできません。
光学収差とは、理想的な結像ができないために、画像がボケたり、歪んだり、点像分布関数(PSF)が拡散したりする現象を指し、顕微鏡システムの分解能が低下する原因になります。例えば、理論上の分解能が200nmであったとしも、光学収差を適切に制御しないと、実際の分解能は300nmまで低下してしまいます。
スネルの法則によると、光には境界面で屈折する性質がありますが、それでもすべての光が一点に集まるわけではありません。スネルの法則に従ってレンズを設計したとしても、レンズ製造時の許容公差(形状・材料のバラつき、組み立て時の誤差など)によって光の波面に歪みが生じ、集光位置がずれてしまうのです。
光学収差は、不可避の物理現象であるものの、適切な対策を実施すれば、その影響を最小限に抑えることができます。
光学収差と開口数の関係性
開口数が大きいほど分解能は向上しますが、同時に光学収差も増大するため、顕微鏡システムを設計する際には注意が必要です。
以下の図にある通り、開口数を大きくすると光量が増加しますが、レンズの周辺部を通る光が強く屈折するため、光学収差が増大します。レンズの中央部のみを使用することも可能ですが、その場合は集光力が低下してしまいます。
光学収差を抑えるには、分解能の許容範囲内で開口数を小さくするか、開口数を小さくできない場合は、非球面レンズや複合レンズを使用するとよいでしょう。


4. ナイキストの定理:最終的な画質の指標
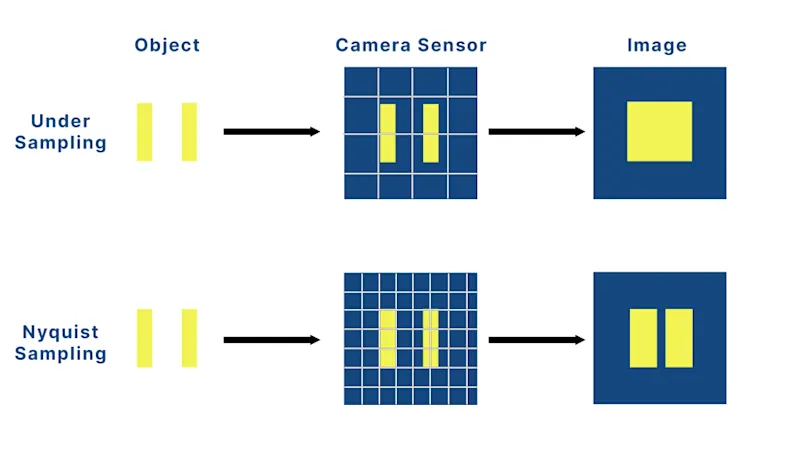
回折限界と光学収差が光学的な結像限界に関係しているのに対し、ナイキストの定理(標本化定理)はカメラの最小検出サイズ、つまり最終的な画質に関係しています。
画像処理の世界において、ナイキストの定理は、画像成分を正確に復元できるかどうかの指標になります。この定理によると、標本化周波数は、必要分解能の2倍以上でなければなりません。
有効標本化間隔≦分解能÷2
言い換えると、下記のようになります。
有効標本化間隔=カメラのピクセルサイズ÷倍率≦d÷2
センサーに像が投影された時、連続する光(アナログ信号)を離散的な画素の集合(デジタル信号)に変換することを標本化(サンプリング)といいます。ピクセルサイズが大きすぎる(アンダーサンプリング)場合、高周波成分が低周波成分として誤って復元され、エイリアシング(画像のブレ、エッジ部のジャギー(階段状のギザギザ)、モアレ(干渉縞)など)が発生するため、微細な構造物を可視化できません。
安全係数Kの追加
ナイキストの定理によると、必要分解能の2倍以上の標本化周波数があれば、理論上は問題ありません。しかし、エッジ部の画像不具合、光学収差、ノイズ、MTF(変調伝達関数)の低下、照明のバラつきなどに対処するには、設計時にある程度の余裕を持たせる必要があります。そのため、以下のように計算式に安全係数K(1.1~1.3)を追加するとよいでしょう。
カメラのピクセルサイズ÷倍率≦d÷(2K)
なお、Kの平均値(=1.15)を使用すると、業界内で一般的な乗数(=2.3)が導き出されます。
5. 計算式の実用例:2μmの欠陥検出
これまでに紹介した計算式を活用し、2μmの欠陥を正確に検出できる顕微鏡システムを設計してみましょう。以下の手順に従えば、分解能に配慮しながら、各種システム要件を決定できます。
手順 | 目的 | 計算方法・結果 |
|---|---|---|
1 | 必要分解能の決定 | レイリー基準の計算式:d=0.61λ/NA(550nmの緑色光) 2μmの欠陥検出に必要な開口数:NA≧0.17 余裕を持たせてNA=0.3とした場合:理論上の分解能≒1.1μm |
2 | レンズの選定(レンズの設計) | 対物レンズの開口数:NA≧0.3 非球面レンズや複合レンズを使用すれば、光学収差を最小限に抑えながら、回折限界に近い性能を実現できます。 |
3 | 標本化間隔の決定 | ナイキストの定理の計算式に安全係数K(=1.15)を追加 有効標本化間隔≦ 2μm÷(2×1.15)≒0.87μm |
4 | カメラのピクセルサイズと倍率の決定 | 有効標本化間隔≦0.87μmの場合 ※ピクセルサイズが小さいほど、倍率を低くできるため、視野角が広がります。 |
顕微鏡システムの分解能とピクセルサイズの対応表
対物レンズの倍率 (開口数) | 分解能 (µm) | 像サイズ (µm) | ピクセルサイズ (µm) |
1×(0.04) | 6.9 | 6.9 | 3.5 |
|---|---|---|---|
2×(0.06) | 4.6 | 9.2 | 4.6 |
2×(0.10) | 2.8 | 5.6 | 2.8 |
4×(0.10) | 2.8 | 11.2 | 5.6 |
4×(0.12) | 2.3 | 9.2 | 4.6 |
4×(0.20) | 1.4 | 5.6 | 2.8 |
10×(0.25) | 1.1 | 11.0 | 5.5 |
10×(0.30) | 0.92 | 9.2 | 4.6 |
10×(0.45) | 0.61 | 6.1 | 3.0 |
20×(0.40) | 0.69 | 13.8 | 6.9 |
20×(0.50) | 0.55 | 11.0 | 5.5 |
20×(0.75) | 0.37 | 7.4 | 3.7 |
6. 業界別事例:半導体検査

半導体検査において、サブミクロン単位の欠陥検出や寸法測定、重ね合わせの位置調整を行うには、高精細顕微鏡システムが欠かせません。上記で解説した回折限界、レイリー基準、光学収差、ナイキストの定理は、半導体の製造工程における外観検査の精度を大きく左右します。
まず、回折限界とレイリー基準は、限界分解能を示す指標として、光の波長や開口数の決定に役立ちます。次に、撮影時の画質に影響を及ぼし、検査精度を低下させる光学収差については、特殊なレンズの使用や配置調整を含め、適切な対策が実施するとよいでしょう。最後に、ナイキストの定理に従えば、分解能に対応したピクセルサイズと倍率がわかるため、エイリアシングを防止しながら、ウエハー上の微細な構造物を正確に捉えられます。

上記の4つの要因以外に、MTF(変調伝達関数)、光のコヒーレンス(可干渉性)、被写界深度、SN比(信号対ノイズ比)、対象物の表面特性、周囲の環境変化なども、実際の製造現場における最終的な撮像性能に影響します。ウエハー表面検査、重ね合わせ測定をはじめ、多岐にわたる半導体検査において、サブミクロン単位の精度と一貫性を実現するには、これらすべてを網羅する高い技術力が欠かせません。
このほか、半導体検査装置を開発する際には、初期設計、試作品の作成から製造現場への設置に至るまで、全工程において徹底した試験と調整を実施する必要もあります。光学に関する豊富な知識と経験を兼ね備えたビジョンエンジニアがいれば、あらゆる要素を総合的に考慮しながら、最適なソリューションをスムーズに導入できるでしょう。
個別のご相談・お問い合わせはこちら