究竟有哪些因素會限制顯微鏡的解析度?
解釋繞射、瑞利(Rayleigh)準則、像差和奈奎斯特取樣
探索顯微鏡解析度的理論與實際限制,讓視覺工程師掌握評估光學限制與指定高解析度成像系統需求的基本知識。

深入了解
Airy 如需清楚瞭解放大倍率、數值孔徑 (NA) 以及這些因素如何影響解析度和影像品質,請先閱讀基礎文章:《放大倍率、數值孔徑 (NA) 和顯微鏡成像的解析度》。
前往文章:《放大倍率、數值孔徑與解析度》1. 了解顯微鏡的解析度
光學顯微鏡的解析度,是指成像系統清晰分辨樣品細節的能力。在半導體檢測等高精度應用中,光學解析度是決定系統效能的關鍵要素。然而,無論相機感光元件有多少畫素,最後能夠解析的最小特徵尺寸,均會受到基本光學解析度的限制。
為了了解並克服這些限制,我們需要了解四個相互關聯的核心概念:「阿貝繞射極限」(Abbe Diffraction Limit)、「瑞利準則」(Rayleigh Criterion)、「光學像差」(Optical Aberrations) 和「奈奎斯特取樣」(Nyquist Sampling)。
2. 繞射:基本物理限制

阿貝繞射極限
阿貝繞射極限描述了光學解析度的基本物理障礙,這是來自於光的波動性所。繞射是一種無法避免的物理極限。在 1873 年,恩斯特・阿貝 (Ernst Abbe) 提出此限制的定量描述,以 d = λ /(2*NA) 表示。
在此:
d 是可解析的最小特徵尺寸 (解析度)
λ 是光源的波長
根據這個等式,使用較短的波長和較高光學的 數值孔徑 (NA) 可提高解析度。NA 取決於成像介質的折射率和最大集光角。
例如,使用 500 nm 光源與 1.4 NA 油浸物鏡,可以得到接近 179 nm 的理想極限。然而,多色照明和鏡頭設計等實際限制,通常會導致實際系統中可達到的橫向解析度為 ~200 nm。
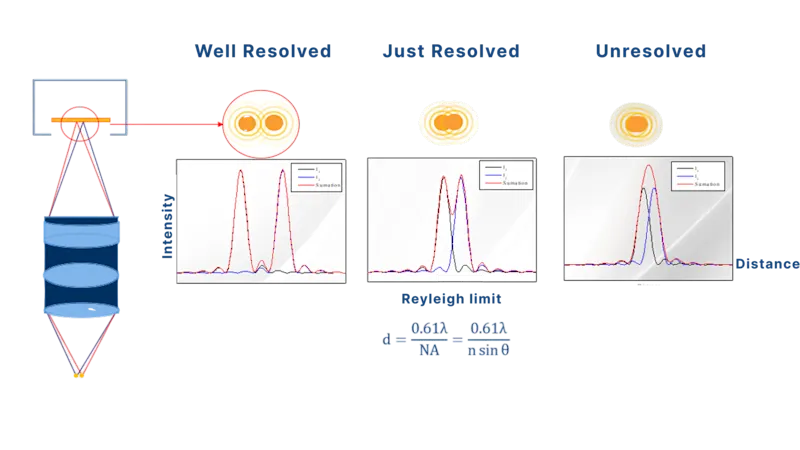
瑞利準則
雖然 Abbe 公式給出了解析度的理論下限,但實際系統也需要一個準則來判斷何時兩個點剛剛好「可分開辨別」。瑞利準則的定義是:當一個艾利盤的中心峰值與另一個的第一個暗環重合時,兩個點光源就是可分辨的:d = 0.61λ / NA
瑞利準則特別適用於評估在部分相干或不相干光源下孤立特徵的可見度,例如用於微粒偵測或污染分析。常見如「解析度 (Rayleigh):0.85 µm at 550 nm」的規格,可確保可靠的自動檢測具備有足夠的對比度。
阿貝公式對光學系統能傳輸的最細微空間細節進行定義,來設定出理論解析度的極限,而瑞利準則對於何時能可靠區分真實影像中的兩個特徵提供了實際臨界值。這兩個概念是互補的:阿貝公式會引導光源波長和物像 NA 等選擇,來設定系統的基本限制,而瑞利準則會確保這些限制能轉化為實際中可用的對比度和可分離性。在設計平衡解析度與影像品質的光學系統時,兩者必須一併考慮。
3. 像差:真實世界的實際限制
即使是理論上符合阿貝限制或瑞利準則的系統,在現實世界中也面臨著嚴峻的挑戰,也就是「光學像差」。
光學像差是一種完美聚焦的偏差,造成影像模糊、扭曲或擴大點擴散函數 (PSF),進而降低有效解析度。一個設計解析度為 200 nm 的系統,在光學像差控制不佳的情況下,解析度可能只有 300 nm 甚至更低。
出現這些像差的原因是,雖然斯涅爾折射定律描述了光線在表面折射的方式,但無法確保所有來自被攝主體的光線,都能完美地匯聚到單一影像點。設計符合斯涅爾法則的鏡片,要同時達到所有光線的完美成像,是極大的挑戰;而且真實的鏡片不可避免地會有變形、材料不均勻性和組裝公差等瑕疵,這些瑕疵會造成波前失真,使光線難以精確集中。
光學像差是一個無法避免的實際限制,但精密工程設計可以將其影響降至最低。
光圈與像差的取捨
理論上,較大的光圈可提高解析度,但實際上卻會使像差惡化;這是一種基本的設計妥協。
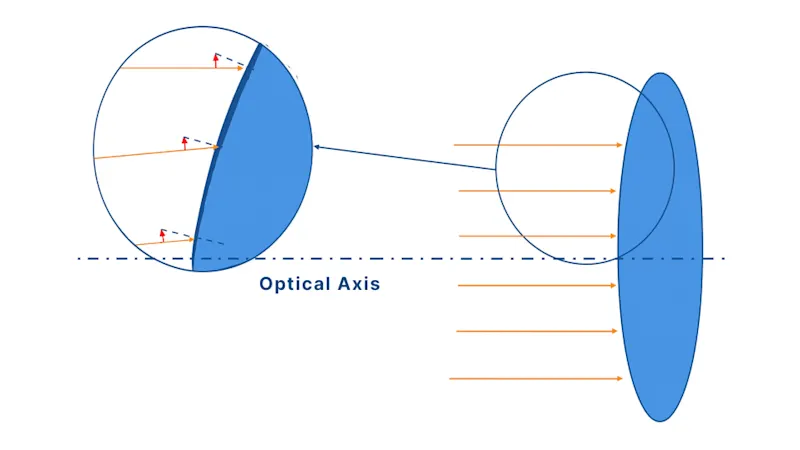
下圖顯示較大的光圈可以讓更多的光線通過,但卻會造成周邊光線在極端角度時產生較大的像差。只使用鏡頭中心可以減少像差,但卻限制了集光能力。
解決方案:尋找能達到解析度與像差平衡的最佳數值孔徑,或使用非球面鏡片和多元件鏡片組合來補償像差,同時維持較大的光圈。


4. 奈奎斯特取樣準則:最終的檢測極限
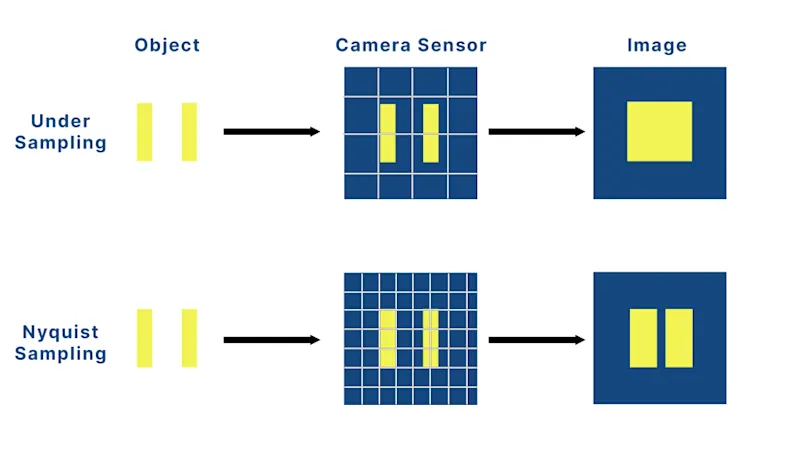
雖然繞射與像差界定了解析度的光學極限,但最終的影像品質還是取決於感光元件是否能真正拍攝到這些細節。這就是奈奎斯特取樣準則(Nyquist Sampling Criterion)發揮作用之處。
此準則指出若要在成像時精確地重建空間細節,取樣頻率必須至少是所需解析度的兩倍。奈奎斯特定理要求:
有效取樣距離 ≤ 光學解析度/2
也就是:
有效取樣距離 = 相機畫素大小/放大倍率 ≤ d/2
當光學影像在感光元件上進行成像時,連續的光分佈會被離散的畫素陣列進行取樣。如果畫素過大 (取樣不足),系統就無法解析成像細節,造成混疊現象 (aliasing),亦即高頻結構顯示為低頻偽像。這會造成影像模糊、邊緣鋸齒和假摩爾纹。
實用設計會考慮安全係數
雖然 Nyquist 理論上需要準確的 2 倍取樣,但實際的設計需要額外的餘量來應付邊緣效應、像差、雜訊、不完美的光學 MTF 以及不同的光源條件。視覺工程師通常會加入約 1.1-1.3 的經驗安全係數 K,將公式修改為
相機畫素大小/放大倍率 ≤ d/(2K)
使用 K = 1.15 的中間值,會得到常用的產業乘數 2.3。
5.從公式到設計:偵測出 2 μm 的瑕疵
現在讓我們將這些公式應用在一個具體的顯微鏡範例中:設計一個系統來可靠地檢測出 2 μm 大小的缺陷。以下步驟展示了這些解析度極限,如何在實際的設計決策中共同發揮作用。
步驟 | 任務 | 行動與結果 |
|---|---|---|
1 | 計算所需的光學解析度 | 使用瑞利準則:d = 0.61λ/NA 搭配 550 奈米綠光。 適用於 2 μm 解析度:NA ≥ 0.17。 選擇 NA = 0.3 作為設計餘量,理論解析度≈ 1.1 μm。 |
2 | 選擇或設計光學元件 | 請選擇 NA ≥ 0.3 的物鏡。 使用非球面元件或多元件設計,將像差減至最低,以達到繞射限制的效能。 |
3 | 計算取樣需求 | 使用奈奎斯特準則與安全係數 (K = 1.15) 有效畫素尺寸 ≤ 2 μm / (2 × 1.15) ≈ 0.87 μm。 |
4 | 選擇相機和放大倍率 | 要達到≤ 0.87 μm 的取樣間距: 注意:畫素越小,放大倍率越低,視野越大。 |
所需的畫素大小與顯微鏡光學解析度相符
目標 (數值孔徑) | 解析度限制 (µm) | 預計尺寸 (µm) | 所需的畫素大小 (µm) |
1× (0.04) | 6.9 | 6.9 | 3.5 |
|---|---|---|---|
2× (0.06) | 4.6 | 9.2 | 4.6 |
2× (0.10) | 2.8 | 5.6 | 2.8 |
4× (0.10) | 2.8 | 11.2 | 5.6 |
4× (0.12) | 2.3 | 9.2 | 4.6 |
4× (0.20) | 1.4 | 5.6 | 2.8 |
10× (0.25) | 1.1 | 11.0 | 5.5 |
10× (0.30) | 0.92 | 9.2 | 4.6 |
10× (0.45) | 0.61 | 6.1 | 3.0 |
20× (0.40) | 0.69 | 13.8 | 6.9 |
20× (0.50) | 0.55 | 11.0 | 5.5 |
20× (0.75) | 0.37 | 7.4 | 3.7 |
6. 產業實作:半導體檢測

在半導體檢測,進行偵測次微米的缺陷、驗證關鍵尺寸以及確保精確的疊層對齊時,高解析度顯微鏡是不可或缺的設備。本文所討論的所有限制:繞射、瑞利準則、像差和奈奎斯特取樣,都直接影響半導體製造光學檢測系統的設計。
繞射極限與瑞利極限定義了光學所能解析的理論最小特徵尺寸,並設定了光源波長與數值孔徑 (NA) 的要求。如果不小心應對,像差會造成實際世界的偏差,降低解析度與量測精準度,因此必須採用先進的鏡頭設計與精確的對準。奈奎斯特取樣可確保一旦達到光學解析度,相機的畫素尺寸和系統放大倍率便能正確拍攝晶圓上的細節,不會出現混疊現象。

但僅有這些原則,並不能保證生產線成功運作。仍有其他關鍵因素,例如系統的調變轉換函數(MTF)光源一致性、景深、訊噪比 (SNR)、樣品表面特性和環境穩定性,都會影響最終的成像性能。對於大面積晶片掃描或覆層計量等半導體檢測任務,一致的次微米精度需要極精確的系統等級工程。
從理論設計到實驗室原型,再到工廠現場部署,需要平衡這些因素、進行廣泛測試,並針對實際生產條件來改善設定。這就是為什麼要建立可靠的半導體檢測系統,不只需要了解光學理論,還需要與經驗豐富的視覺工程師合作,將所有因素整合,擬出強大、可運用於生產的解決方案。
有特定專案的光學方面問題?請向我們經驗豐富的工程師諮詢。