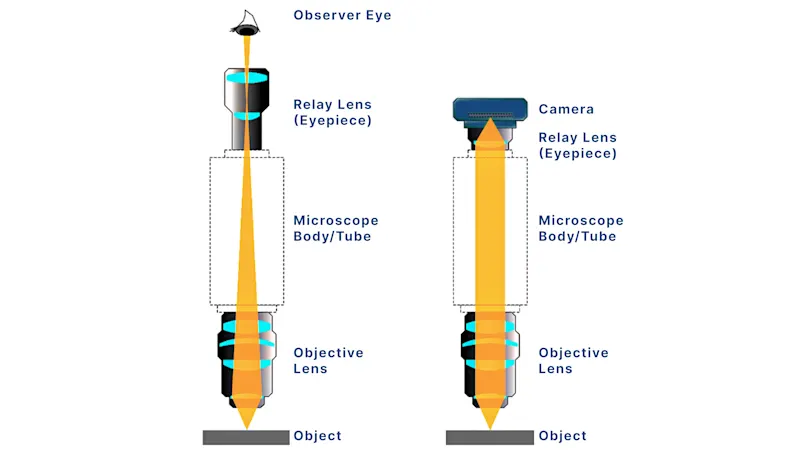
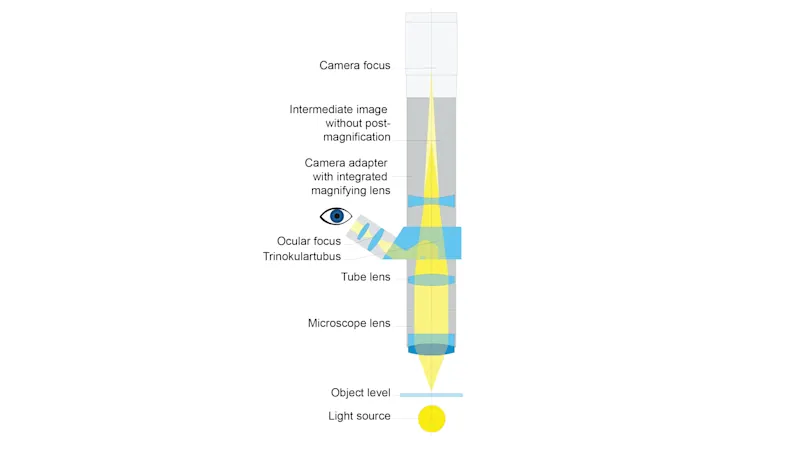
顯微成像中的放大倍率、數值孔徑（NA）與解析度
在顯微成像中，工程師常將放大倍率與解析度混淆，誤以為提高放大倍率即可顯示更細微的細節。這種誤解會導致系統配置效率低落，並在半導體檢測、生醫成像與精密量測等關鍵應用中遺漏重要特徵。本文將釐清放大倍率、數值孔徑（NA）與解析度之間的關係，並引導視覺工程師設計適用於微米與次微米等級的高效能視覺系統。
顯微成像中的放大倍率
顯微成像的本質是運用放大倍率的原理，以觀察樣本的放大影像。放大倍率分為兩種類型：
1. 光學放大倍率
光學放大是在影像到達感光元件之前將其物理放大。這是透過物鏡和管鏡的共同作用來實現的。當計算系統放大倍率時，您可以根據您的設定採用下列兩種方法之一 - 標準製造商物鏡或客製化鏡頭組合。
A. 使用製造商規格（標準系統）
在大多數採用無限遠校正光學系統的工業或研究型顯微鏡中，物鏡會標示一個名義放大倍率（例如 10×、20×、50×）。此放大倍率是以標準的鏡筒透鏡焦距為基準進行計算，通常為 200 mm，但也有部分製造商採用 180 mm 或 165 mm。
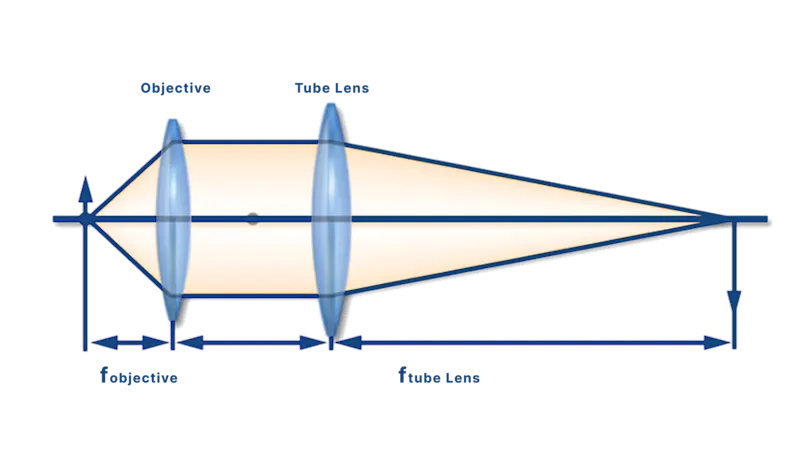
B. 直接使用焦距計算（客製或 OEM 光學系統）
在許多 OEM 或客製化視覺系統（例如機器視覺）中，工程師經常不使用廠商提供的放大倍率，而是依據基礎光學原理直接計算放大倍率：
Msystem=ftube lens / fobjective
其中：
ftube lens: 鏡筒鏡頭或中繼鏡頭的焦距
fobjective: 物鏡的焦距
此方法在整合客製化光學元件或設計無標準元件的精巧系統時，具備高度彈性。
範例：
搭配 20 mm 物鏡的 200 mm 鏡筒可得放大倍率 M = 200 / 20 = 10×
若改用 100 mm 鏡筒則為 M = 100 / 20 = 5×
鏡筒或轉接鏡常標示為 0.5×、1×、2× 等，這些倍率對應的即是其根據上述焦距比所縮放的影像比例。
在建構視覺系統時，標準架構可採用廠商提供的公式，客製化設計則建議使用焦距比計算方式，特別適用於 OEM 與機器視覺應用。兩種方法在一致應用下都具備高度準確性，關鍵在於選擇最符合系統整合與效能目標的模型。
設計時的重要考量：
較高的有效放大倍率會減少視野範圍（FoV），在進行大面積檢測時可能需進行更多影像拼接。
若只提高放大倍率而不增加數值孔徑（NA），並不會提升解析度，僅是將相同的解析度分散至更多畫素（即過取樣）。
系統設計應符合奈奎斯特取樣原則—每個最小可分辨特徵至少需覆蓋 2 個像素，才能避免混疊現象。
然而，實際需求仍取決於應用情境：
若目的是檢測粒子（例如有無判斷），則 1 µm/像素的解析度可能已足夠。
若目標是檢查形狀、邊緣或精細圖樣，則必須遵循奈奎斯特取樣原則，以準確解析細節並避免資訊流失。
範例：
若使用像素尺寸為 3.45 µm 的 500 萬畫素相機成像 1 µm 的細節，則至少需要：
3.45 µm / 1 µm = 3.45 ⇒ 需要至少 6.9× 的放大倍率
這可確保每個 1 µm 的特徵在感光元件上至少覆蓋 6.9 µm，符合 2 像素原則的取樣需求。
2.
指透過像素插值來人為放大影像區域的後處理技術 (例如數位變焦)。與光學放大不同，它不會增加新的空間資訊，通常：
降低有效解析度
產生像素內插失真
不適用於如半導體檢測等高精度應用
因此，數位放大僅應用於影像視覺化呈現，不建議用於關鍵量測或檢測工作。
解析度與數值孔徑 (NA)
雖然放大倍率決定影像中特徵在感光元件上的呈現大小，但真正影響系統解析微細細節能力的關鍵，是數值孔徑（NA）。本段將說明 NA 如何影響解析度，以及如何針對不同成像情境進行最佳化調整。
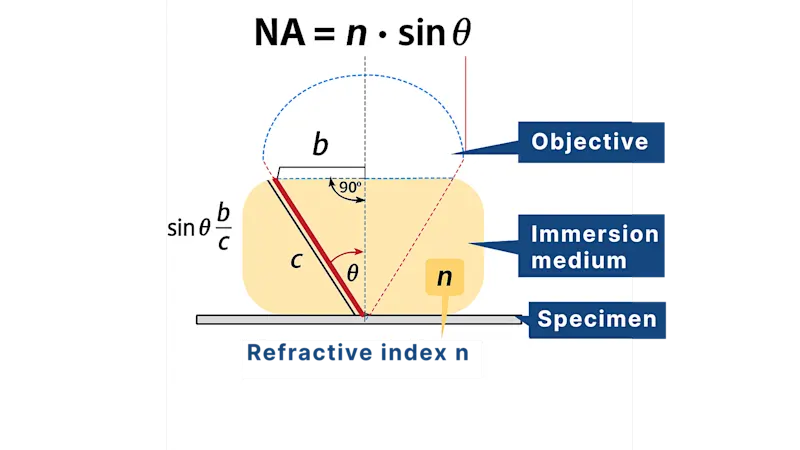
NA 是什麼？
數值光圈 (NA) 量度鏡頭收集光線和解析細節的能力。它直接影響解析度、影像銳利度和亮度。NA 值越大，結果影像的解析度就越高。NA 的計算方式如下
NA = n sin 𝜃
其中：
n：物鏡與樣品之間介質的折射率（空氣為 1.0，油約為 1.5）
𝜃：鏡頭所收集光錐的半角角度
NA 值會在以下情況下提高：
使用比空氣折射率更高的介質（例如浸油或水）時。
增加光圈直徑時。
縮短工作距離，使光線以更陡的角度進入鏡頭時。
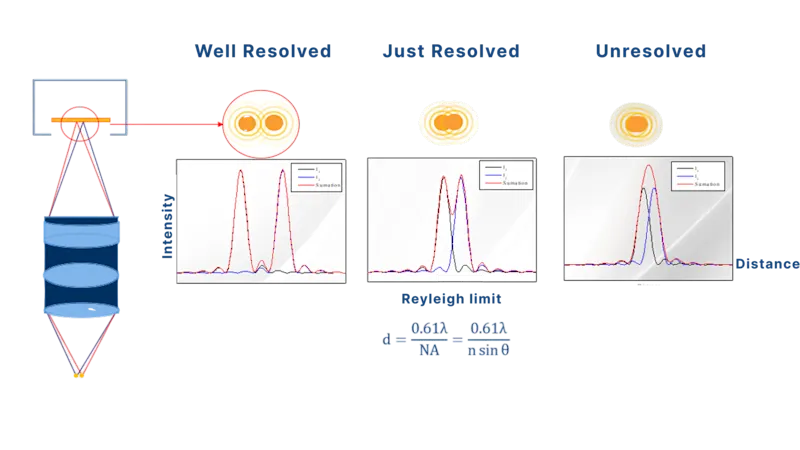
解析度與數值孔徑（NA）的關係
光學解析度受限於繞射效應：
解析度 = 0.61⋅λ / NA = 0.61⋅λ / (n ∙ sin 𝜽)
其中：
λ：照明波長
較高的 NA 可解析更微小的特徵，這對晶圓檢測或精密量測等需邊緣銳利度與精細圖樣區辨能力的應用來說極為關鍵。
然而，光學解析度的提升只有在感光元件的畫素尺寸與放大倍率符合系統解析能力時，才能轉化為可用的影像細節（奈奎斯特取樣必須滿足）。
註: 此解析度公式源自繞射理論與 Rayleigh 判據，其描述光線如何形成如 Airy 環等繞射圖樣。這些概念將在後續深入探討光學繞射與成像極限的文章中詳細說明。
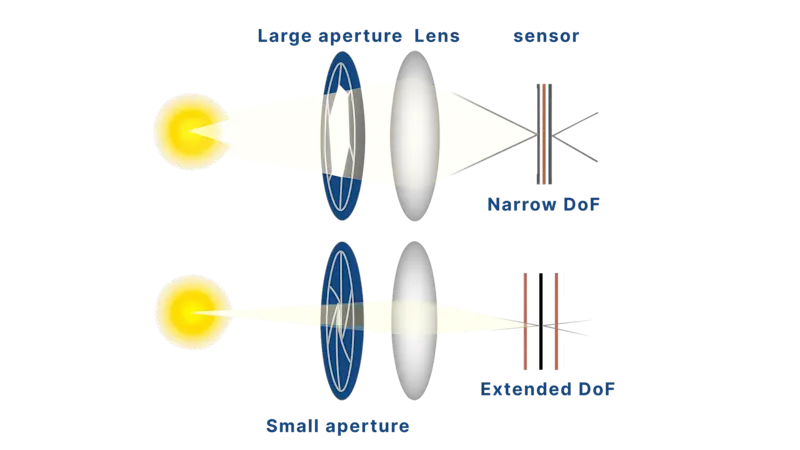
提高 NA 就能解決所有問題嗎？
不盡然。雖然提高 NA 可提升解析度與亮度，但也伴隨以下代價：
工作距離變短，降低可操作性。
景深變淺。
對光學對位與對焦要求更高。
高 NA 鏡頭通常對像差更敏感，且價格更高。
此外，NA 也會與影像端光學元件互相影響（詳見下一節），進而影響影像對比與整體系統保真度。
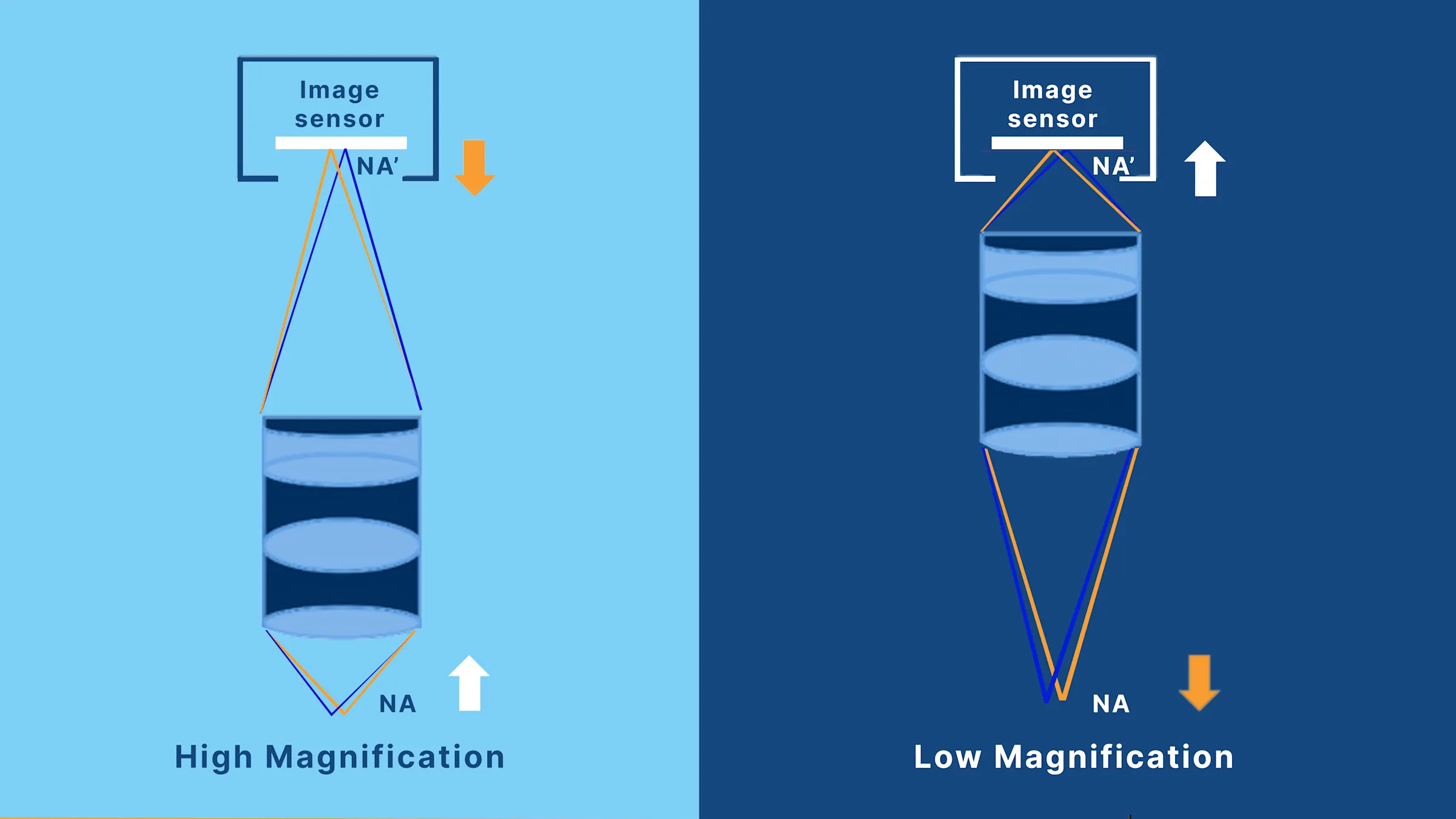
物側與像側數值孔徑（NA）的比較
完整的成像系統包括物體側和影像側的數值孔徑，各自影響不同的影像品質。
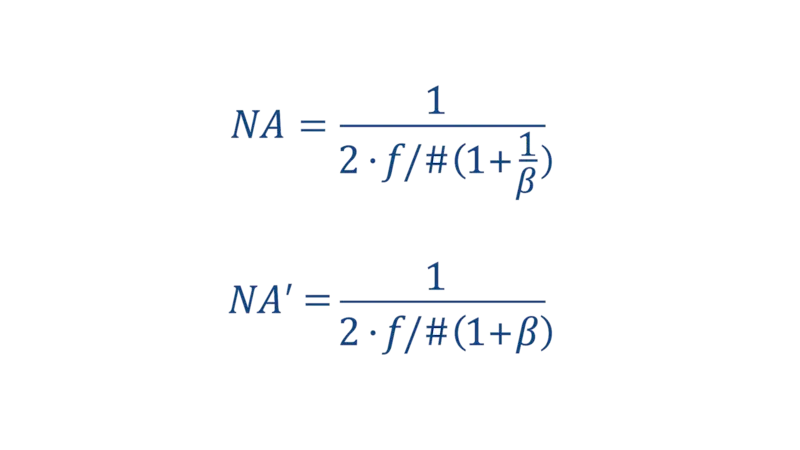
定義與公式
NA（數值孔徑）分為兩種類型：
物側 NA（NA）：位於樣品與物鏡之間
像側 NA（NA′）：位於鏡筒鏡頭與感光元件之間
這兩個 NA 之間的關係可由以下公式表示：
NA = β X NA'
其中：
β：表示橫向放大倍率，定義為影像尺寸除以物體尺寸。
這代表隨著放大倍率上升，物側 NA 會增加，而像側 NA 則會下降。實務上，為了解析較小的缺陷，通常會提高放大倍率以取得較大的物側 NA。然而，這也會導致像側 NA 降低，進而使影像變暗、變模糊。
物側 NA 與像側 NA′ 的取捨關係
這種反比關係對系統設計至關重要：
NA 控制系統可解析的最小特徵尺寸。
NA′ 則決定該特徵被傳送至感光元件時的清晰程度，也就是影像的對比度，特別是在高空間頻率下。
NA′ 與 調變傳遞函數（MTF） 有密切關聯—MTF 是用來衡量不同特徵尺寸下的對比度表現。若 NA′ 過低：
在高頻率下，MTF 將急遽下降。
即使在技術上可被解析，細節也可能變得難以辨識，甚至完全不可見。
簡而言之，若僅有高 NA 而 NA′ 不足，將可能產生看似銳利但缺乏足夠對比的影像，無法滿足穩定檢測或精確量測的需求。
結論
在顯微成像中，放大倍率、數值孔徑（NA）與解析度必須共同協調，單獨優化其中一項，並無法保證影像品質提升。
放大倍率決定影像中特徵在感光元件上的呈現大小，需與相機的像素尺寸匹配，才能避免過取樣或取樣不足。
NA（數值孔徑）決定鏡頭可解析的最小特徵尺寸。較高的 NA 可提升細節還原與亮度，但會犧牲景深。
NA′（像側數值孔徑）影響細節傳遞至感光元件的清晰程度，特別是在高空間頻率下，對影像對比與可視性有顯著影響。
重點總結：高放大倍率需搭配高 NA 才能達到應有解析度，而兩者都需具備足夠的 NA′ 才能維持影像對比。一個理想的系統應同時兼顧解析度、對比度與視野範圍。